Math is for Babies: You’re Never too Young to Start...

When I was teaching math, I worked with many students like Olivia. She was a sophomore in high school and wanted to be an actress; her parents were artists; her brother was, without hyperbole, a guitar prodigy. Olivia’s family needed art like plants need the sun and, in an unfortunately common pairing, they all shared a distaste for mathematics.

I spent much of my teaching career thinking about students like Olivia. By the time they reached me, by high school, their anti-math tendencies ran deep. By age fifteen or sixteen, my anti-math students had nearly two decades of math-negative signaling: parents who disliked math, dull curricula, and a predominant culture in the United States that treats math like magic instead of an accessible tool that everyone should learn to use (there is a lot of good discussion about this: try reading Petra Bonfert-Taylor’s Washington Post article about math culture). Sometimes I had a student like Olivia who actually believed me when I told her she could do math, who took the leap of faith and boarded my magic (not magic) carpet of math exploration. But just as often, my attempts to spark excitement and curiosity about mathematics in my anti-math students fell short.

I began training to become a neuroscientist in part because of these students. I dwelled often on their brains compared to the brains of the math-lovers in my classes. I wondered how early in development children start to build concepts related to number, and how early differences in numerical development might begin that will, later on, manifest in school. I’ll get to their brains in a moment, but the first thing I realized–and many of you know this already–is that confidence and curiosity in mathematics can, and should, start young. From birth, even. Starting on day one, parents have the opportunity to promote an appreciation, if not a love, of mathematics¹.

Since I just proposed doing math with infants, many of you probably stopped reading. But if you’re still with me, I learned three main ideas from education and neuroscience that brought me to this conclusion:

1. There is a large consensus on promoting language and literacy from birth. The principles for promoting mathematics are tremendously similar.
2. Plenty of evidence demonstrates how mathematical skills can be just as or more important than language skills in measurements of future success².
3. Unlike reading or speaking, babies already do math (well, they are at least able to discriminate between sets of two and three objects³).

Reading for babies

Head Start launched in 1965 in the United States as a program that supported disadvantaged preschool children and their families. Initially an eight-week summer program, Head Start grew to become an essential provider of early childhood support throughout the year, with classes, services, and outreach programs (Sesame Street, in fact, launched under Head Start funding in 1969). Importantly, Early Head Start was formed in 1994 to serve children ages zero to three–in response to research that indicated the importance of these years to cognitive, physical, and emotional growth.

This idea, that the first three years of life may be more important for future development than, say, ages seven to ten, has taken root in the world of reading and language development. For example, some parents and researchers have become very familiar with the following figures, summarizing some of the work by Hart and Risley, who provide evidence that oral language enrichment from birth affects later language development:

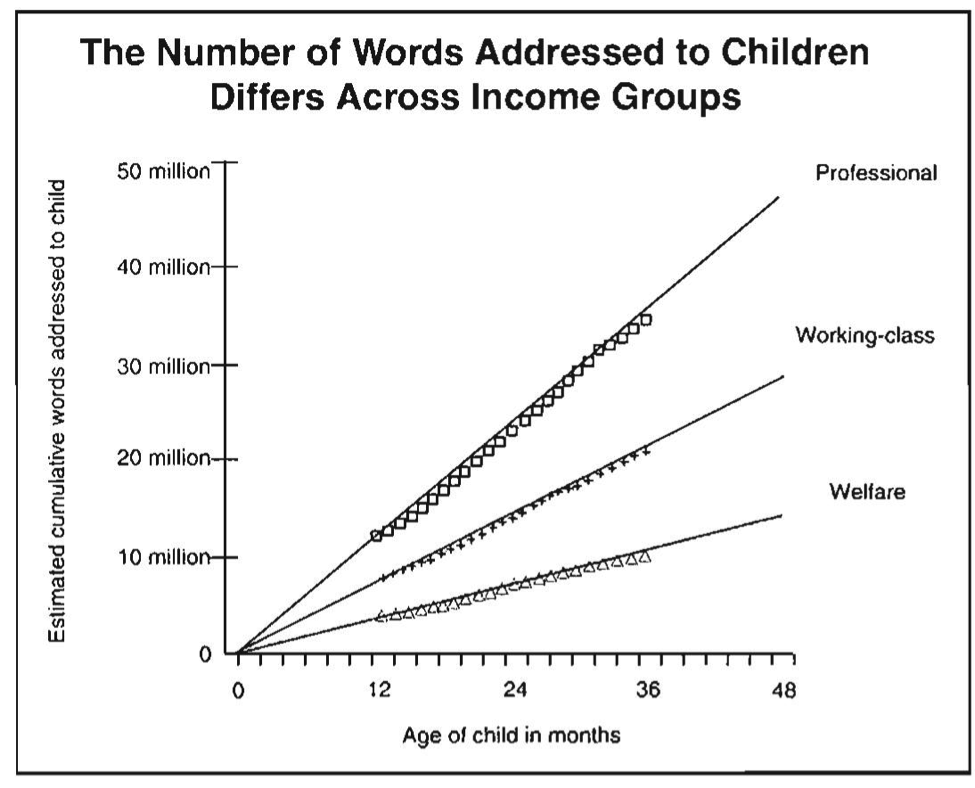
Figure 1. Hart and Risley’s4 research found that at higher levels of socioeconomic status (SES), children were exposed to more words (by volume) in their first three years. They referred to this phenomenon by the mnemonic “30 million words by age three”–i.e., by age three there is a difference of 30 million words heard when comparing high and low SES groups.

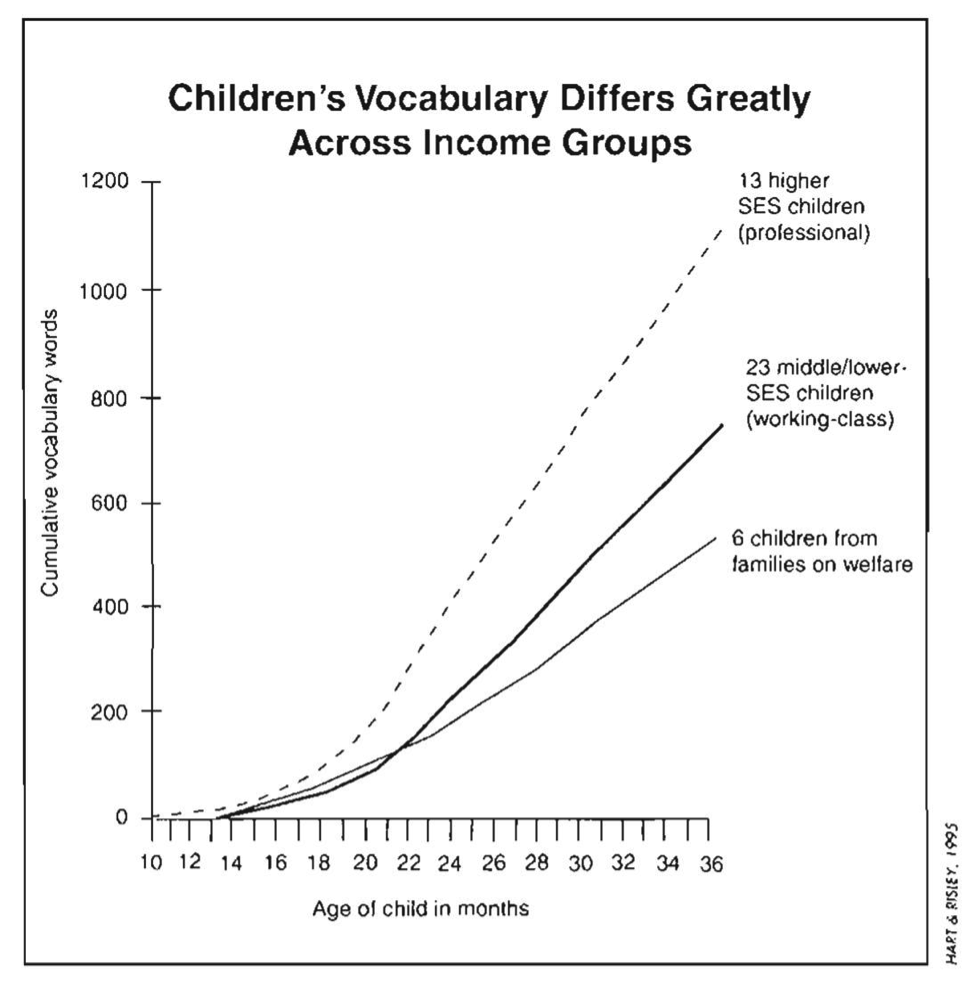
Figure 2: Hart and Risley note that difference in language received correlates to children’s productive vocabulary, suggesting that exposure to oral language skills from birth are important for future language development.

Nowadays, I meet many parents who know the importance of “language nutrition” (to steal a phrase from Rose Hendricks’ article on this subject) and even know the importance of speaking to their infants. My brother and his wife, with their first child, knew that they should speak as much as possible with their newborn, even if they didn’t quite know why.

I’m not writing about reading, however. I’m writing about math. And my point is simple: just as early exposure to oral language is important for language development and later reading, so is early exposure to numerical thinking to later math ability and appreciation. When children see their parents reading every evening, they (often) learn a love of reading. When children see their parents interact with and promote numerical thinking, they (often) learn a love of math.

Skwarchuk, Sowinski, and LeFevre⁵ studied the home environments of four-year-olds and looked for correlations to numeracy and literacy scores one year later. They found that formal home numeracy practices predicted children’s knowledge of the symbolic number system and exposure to games with numerical content predicted children’s non-symbolic arithmetic. Another study from Libertus, Feigenson, and Halberda⁶ found evidence that in three- to five-year-olds, early understanding of small numerical quantities correlated to later mathematical ability.

In summary, research and practice both support language and literacy development from birth. Research also provides evidence supporting numerical development from birth, but in my experience I have not observed an equivalent excitement for numerical development in the United States. I propose that we, as a culture, shift to show babies a world filled with oral language and numerical thinking.

Math can affect later outcomes as much as reading!

Duncan and colleagues², in a longitudinal study of students from school entry to age 14, found that school-entry numerical skills correlated with later academic achievement more than school-entry language skills. The authors write, “Before they enter preschool, children vary greatly in their numerical and mathematical knowledge, and this knowledge predicts their achievement throughout elementary school.” In another study from the National Research and Development Centre for adult literacy and numeracy in England⁷, researchers analyzed a massive longitudinal data set that followed infants from birth to ages past 30. They found that early numeracy and literacy both contributed to several outcomes in adulthood such as high-school drop-out rate, level of education achieved, rate of employment, and salary. In some subgroups, numeracy, more than literacy, predicted economic well-being, rate of home ownership, and even conflicts with authority.

It is important to note that early numeracy and literacy are not the only measures that correlate with later outcomes. In the studies discussed above, the comparison between numeracy and literacy controls for other important factors such as socio-economic status, which has a strong correlation with all cognitive skills⁸. My point here is simply that early numerical ability is important for future development–not just in mathematics but towards significant life outcomes. I argue that this correlation between early numeracy and later outcomes is another reason that parents and teachers in the United States should promote numerically rich environments from birth.

Babies already do math

Animals do math. They count, compare quantities and perform basic operations. In a famous study of chimpanzees⁹, for example, subjects were presented with trays with different numbers of chocolate pieces, and they consistently chose the tray with the greater number. Other experiments have tested animals using different senses (hearing, touch, sight, etc.) and paradigms in which the number is independent of the reward: Church and Meck¹⁰, for example, gave rats a lever-pressing task in which rats listened to tones and pressed one lever for two tones and a different lever for four tones. They also found that rats had an innate sense of quantity.

Research exploring the numerical abilities of babies has developed very clever methods for measuring their ability to detect number. Early studies relied on the fact that babies stare longer at novel scenarios^3,11. When presented with two dots over and over, babies would lose interest and stare for less time at each presentation. But when the stimulus changed to three dots, babies would stare at the presentation longer. This kind of result has been shown with infants younger than one year and even in newborns. Later studies introduced different paradigms and better visual and spatial controls, and consistently found that infants detect numerosity¹².

Studies in neuroscience have provided some additional evidence for innate numerical abilities in human infants. For example, Izard and colleagues¹³ tested three-month-old infants by presenting arrays of objects in different combinations of number and identity. They might show, for example, three carrots and later show images with different numbers of carrots or the same number but with different objects. Using event-related electroencephalogram (ERP—this measures electrical activity in the brain after a specific stimulus is presented), they found that neural activity differed for number (i.e., same object but in different quantities) compared to object identity (same quantity but different objects). Number changes were uniquely marked by differences in the right parietal region of the cortex, while identity changes were uniquely marked by differences in the occipito-temporal cortex. Since the right parietal region of the cortex is a region that has been shown in older children and adults to be important for numerical processing, this study provides evidence that even at three months of age, infants may show early neural signatures of numerical ability.

What is math for babies?

Some clues as to which environmental factors are conducive to early numerical development come from studies that compare the effects of culture and language on pre-schooling numerical ability and the correlation of this ability to later academic performance. Many studies, for example, compare native Mandarin to native English households due to interesting differences in culture and language^14,15. These studies note that Mandarin words for numbers are more clear about quantity than English words. For example, the English word “one” can mean the number one, but it can also be expressed in the plural as in “these ones are my favorite”. This ambiguity does not exist for the Mandarin number. The linguistic clarity for Mandarin numbers may contribute to the advantage of Chinese schoolchildren in mathematics compared to those in the United States (reported in the above studies). Other factors include formal education experiences with parents and parental views on the importance of academic learning.

Generally, here are some basic ideas of what a rich numerical environment might involve for infants:

• Frequent parental use of numeric speech, especially speech that identifies the quantities in groups (e.g. three giraffes, ten penguins)
• Frequent subitizing (labeling small sets–groups of one, two, or three items)
• Games, toys, and books that promote numerical and spatial thinking
• Adults who, in the presence of the infant, include numeracy in their discussions and show positive attitudes towards mathematics

While these ideas are not complex or difficult, implementing them will involve changing individual and group-level habits, which can be quite hard, indeed. Changing numerical culture in the United States, however, would be extremely beneficial. Generally, the lesson I’ve gleaned from my years as a teacher and a scientist is: If we want to improve in any domain, we can improve K-12 and higher education (and we should!), but pre-K might be just as important or even more. This is the period during which children are exposed to their new worlds and make unconscious decisions about how the world should be.

In the case of Olivia, my math-phobic high-school student, I believe her distaste for mathematics began when she was born. Her parents, both math-phobic artists, probably avoided math language around her and promoted the arts over numerical games. Her early environment probably cascaded into other influences such as a lack of mathematical enthusiasm in her broader communities and, later, a couple years of negative classroom experiences. I believe, however, it is possible—and easy!—to promote mathematics and the arts or literacy. With newborns, it may be as simple as counting.

References & Further Reading

1. Lefevre, J. A., Kwarchuk, S. L., Smith-Chant, B. L., Fast, L., Kamawar, D., & Bisanz, J. (2009). Home numeracy experiences and children’s math performance in the early school years. Canadian Journal of Behavioural Science, 41(2), 55–66.
2. Duncan, G. J., Dowsett, C. J., Claessens, A., Magnuson, K., Huston, A. C., Klebanov, P., … Japel, C. (2007). School readiness and later achievement. Developmental Psychology, 43(6), 1428–46.
3. Antell, S. E., & Keating, D. P. (1983). Perception of numerical invariance in neonates. Child Development, 54(3), 695–701.
4. Hart, B., & Risley, T. R. (2003). The early catastrophe: The 30 million word gap by age 3. American Educator, 27(1), 1–6.
5. Skwarchuk, S.-L., Sowinski, C., & LeFevre, J.-A. (2014). Formal and informal home learning activities in relation to children’s early numeracy and literacy skills: the development of a home numeracy model. Journal of Experimental Child Psychology, 121, 63–84.
6. Libertus, M. E., Feigenson, L., & Halberda, J. (2011). Preschool acuity of the approximate number system correlates with school math ability. Developmental Science, 14(6), 1292–1300.
7. National Research and Development Centre for Adult Literacy and Numeracy (2005). Does Numeracy Matter More ? London: Parsons, S., & Bynner, J.
8. Lee, V. E., & Burkam, D. T. (2002). Inequality at the starting gate: Social background differences in achievement as children begin school. Washington, D.C.: Economic Policy Institute.
9. Rumbaugh, D. M., Savage-Rumbaugh, S., Hegel, M. T. (1987). Summation in the chimpanzee (Pan troglodytes). Journal of Experimental Psychology: Animal Behavior Processes, 13(2), 107-115.
10. Church, R. M., & Meck, W. H. (1984). The numerical attribute of stimuli. In H. L. Roitblat, T. G. Bever & H. S. Terrace (Eds.), Animal Cognition (pp. 445-464). Hillsdale, New Jersey: Erlbaum.
11. Starkey, P., Cooper, R. G. (1980). Perception of numbers by human infants. Science, 210(4473), 1033-1035.
12. Dehaene, S. (1997). The number sense. New York, NY: Oxford University Press.
13. Izard, V., Dehaene-Lambertz, G., & Dehaene, S. (2008). Distinct cerebral pathways for object identity and number in human infants. PLoS Biology, 6(2), 275–285.
14. Chang, A., Sandhofer, C. M., Adelchanow, L., & Rottman, B. (2011). Parental numeric language input to Mandarin Chinese and English speaking preschool children. Journal of Child Language, 38(2), 341–55.
15. Miller, K. F., Smith, C. M., Zhu, J., & Zhang, H. (1995). Preschool origins of cross-national differences in mathematical competence: The role of number-naming systems. Psychological Science, 6(1), 56–60.

• Risley, T. R., & Hart, B. (1995). Meaningful differences in the everyday experience of young American children. Maryland: Paul H. Brookes Publishing Co.
• Bonfert-Taylor, Petra (2016, April 25). Stop telling kids you’re bad at math. You are spreading math anxiety ‘like a virus.’ The Washington Post.