Confusion is a powerful feeling.
If it doesn’t turn to frustration, it can give rise to curiosity, motivation, and engagement. So why do we tend to think of confusion as a negative feeling, as the opposite of understanding, our goal?
In order to address the roots of the issue, we’ll have to re-examine two of the assumptions in our teaching and curriculum designing.
Assumption 1: The purpose of education is the outcome; students need to learn to solve these problems (write these essays, respond to these questions) correctly.
Assumption 2: The best way to teach students a complex concept is to break it down into manageable chunks.
Let’s tackle the first one first. While we know that successful parroting of knowledge is not the ultimate goal of education (especially in an age where anyone can google the answer to anything), this ideology is a hard one to shake. After all, we cannot peer into the heads of our students and assess them on their process; all we can do is test the degree to which they’ve understood the difficult concepts.
This leads to a very behaviorist way of looking at learning, which assumes that all we can know is the students’ behavior so we should not try to speculate about cognitive processes we cannot see. This does no one any good, as the students may not be learning any transferrable concepts or skills except following directions.
Of course, this works differently for different subjects, but the core idea remains the same. In math it may be the difference between mechanically doing calculations and exploring relationships and representations; in social studies it may be the difference between memorizing dates and understanding the social trends that contributed to historical events; in science it may be the difference between remembering and being able to reconstruct a phylogenetic tree from memory, and understanding the fluid evolutionary process that it represents.
The second assumption comes from a reductionist perspective, which assumes that any whole can be explained by breaking it down into its constituent parts. In other words, the whole is equal to the sum of its parts, and no more. As we are learning from Complex Systems science, it is often not the particular pieces but their relationships and interactions that give a substance its qualities. For example, all of matter is made of the same elements (hydrogen, oxygen, and so on) but it is their different configurations that lead to different materials. Learning all of the steps that make up solving a complex math problem may be like learning the elements that make up metal without ever having the experience of actually touching metal. It does not mean that one understands the relationships between the concepts that they are manipulating.
When students are taught a subject like math in pieces, without seeing how the pieces fit together, it can be discouraging, and make math seem boring and frustrating. If instead, math is taught as an exploration of relationships, with guidance toward noticing patterns, the process can be creative, and can show students the deep beauty of mathematics. For a great example, see Alan Kay’s TED talk.
Further, students do not begin as empty vessels. Rather, they have already built models for understanding the world. Complex concepts are often complex because they are unintuitive, and simply presenting the pieces to students is often not enough for them to truly integrate the ideas with their existing conceptual frameworks.
Taken together, these assumptions lead to the conclusion that confusion is the result of unsuccessful teaching, and not, as research suggests, a valuable catalyst for deeper learning and better retention.
“We are as curriculum designers and teachers and educators, over-engineering the curriculum, and we’re surgically removing the thinking, so that our kids are simply following instructions, painting by the numbers, and getting the grade. We need to get thinking back at every desk.”
Dr. Derek Cabrera in his Ted Talk
* * *
Many teachers are already successfully making this happen in their classrooms, but it is becoming increasingly difficult as they receive pressure from administration, parents, lawmakers, and corporate reformers about what and how they should teach. Reconsidering educational goals and how deep learning could feel may help contribute to a conversation that can align the views of these various stakeholders and create the space teachers need to teach effectively.
In his TED talk, Tim Harford talks about frustrating disruptions leading to improvement in all kinds of tasks from solving a murder mystery to writing a rock and roll album. He talks about how we shy away from creating difficulties for ourselves and in doing so we miss opportunities for greater creativity and learning.
So how can we create an environment of thinking deliberately in our classrooms?
- Repackaging problems to make them active.
Textbook math problems often suffer very severely from the reductionist and behaviorist mindsets described above. This is evident, for example, when math problems take a real-world scenario, convert it to mathematical terms, formulate the question, break the solution down into a step-by-step process, and label the steps a., b., c., and d.
In his Ted Talk, Dan Meyer discusses this process for typical math problems.
“What we’re doing is we are taking a compelling question, a compelling answer, but we’re paving a smooth straight path from one to the other and congratulating our students for how well they can step over the small cracks in the way.”
This illustration is from math class, but of course a similar process it taking place across the curriculum. To “get thinking back at every desk,” as Cabrera describes it, we need to un-pave that path.
Start with the complexity – it will confuse the students – but that confusion can be a good thing.
Guide them as they traverse the difficult terrain between the question and the answer, but do not give in to the temptation of trying to make it as easy and painless as possible, as this will ultimately help no one.
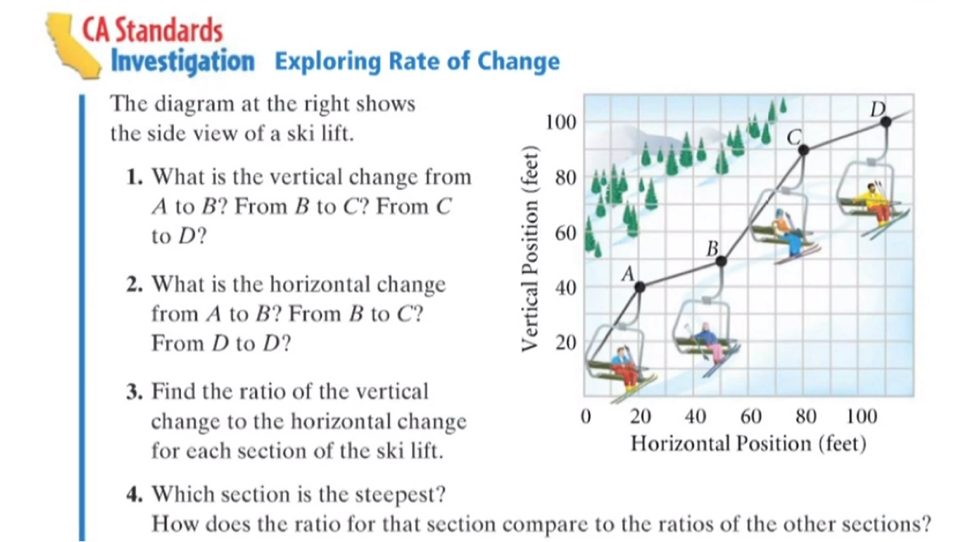
This does not mean that each educator has to reinvent the entire curriculum. It can be as simple as taking off all of the training wheels provided by the design of the question, and collectively rebuilding them together. For example, in his talk Dan Meyer describes taking the problem pictured above and offering students only the visual image of the skiers and the question: which section is the steepest? After discussion, students will generate the idea of labeling the skiers in order to more easily refer to them and overlaying a grid in order to more precisely think about steepness. “The math serves the conversation; the conversation does not serve the math.”
This idea of some sort of struggle as essential to learning has long been known in the research, under the umbrellas and in the manifestations of several different concepts.
- Active Learning: In one meta-analysis of 158 studies, students who learned STEM material by listening to a lecture performed 6% worse on the exam and were 1.5 times more likely to fail than otherwise identical students who learned the same material through active learning.1 Being given the answers (or even the questions!) is significantly less effective for deep learning than figuring that material out for oneself.
- Desirable Difficulty: It is easier to study by packing study sessions together and blocking practicing on the same topic together. However research2 has shown that creating a desirable difficulty in one’s study habits makes the studying more effective. Spacing rather than massing study sessions; interleaving rather than blocking practice on separate topics; varying how to-be-learned material is presented all have better outcomes on memory.
- Disfluency: Better memory for tasks that take more effort can happen due to superficial features such as font. In one study, high school students given material in a difficult font performed better than those given the same material in an easy to read font. This was true across many classes and subjects.3 Even if the extra effort is superficial, it can still make the material more memorable.
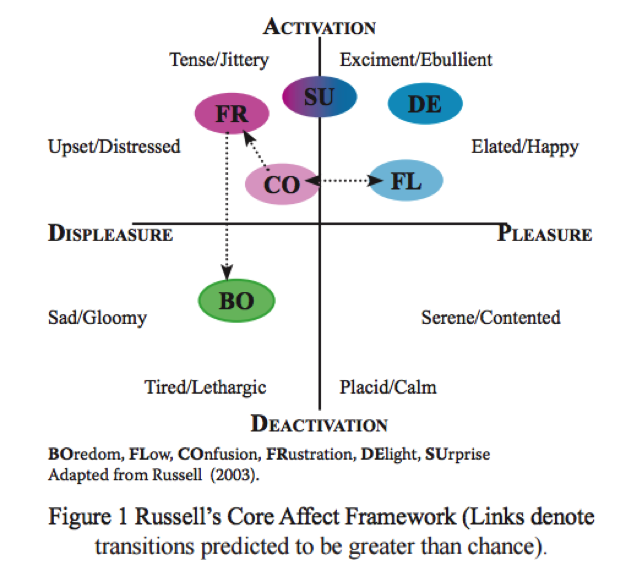
- Russel’s Core Affect Framework: In a study4 that measured change in students’ affect while they learned using a computer tutor, researchers were able to calculate which affective states most often led to which other states.
In the graphic above, the x axis represents valence: on the right is positive and on the left is negative. The y axis represents arousal: on the top is high and on the bottom is low. Boredom, at the bottom, is negative and disengaging, and it is also a dead end as far as affect goes.
Confusion, located in the slightly negative and slightly aroused area can turn into Frustration (if the task is too hard) or it can turn into Flow (if the task is the optimal challenge). This is notably different from what we might consider to be a similar affect — surprise, or a positive affect — delight, which do not predictably lead to any other affective states. In other words, it takes a challenge to enter a state of flow in order to overcome it. The researchers found that Confusion and Flow were positively correlated to learning whereas Boredom was negatively correlated.
- Cognitive Disequilibrium.
As mentioned above, students do not come into a classroom as a blank slate; they have already, consciously and subconsciously, constructed their own ways of understanding the world.
Complex ideas are often complex because they are counterintuitive. Presenting students with information that does not fit into their model will cause them to expend mental effort in order to accommodate or assimilate this information into their schema. That mental effort helps them to learn the material deeply. This idea was embraced by two of the founding fathers of Developmental Psychology: Jean Piaget and Lev Vygotsky.5
Jean Piaget created a model of learning that places disequilibrium at its center. Students avoid disequilibrium because it is an uncomfortable state, and also seek it out because of curiosity; it indicates to them that their model is incomplete. Disequilibrium then leads to accommodation of their mental model to make sense of their new experience, thus updating their mental model.4
Lev Vygotsky coined the idea of the Zone of Proximal Development. This is the set of tasks that a learner is not able to complete on their own, but can complete with some guidance. That extra bit of struggle and challenge makes this the most optimal zone for learning. It is important to note that this zone will be different for different students, and a problem that is in the ZPD for one student may be too easy for another and too difficult for a third.
- Lead with the most Relevant or Beautiful
One reason that students are disengaged is that it is often difficult to see the direct relevance of the material in the textbook with their daily lives.
For this reason there has been a large movement toward project based learning, often with a community service lens. For example, many schools have implemented projects that teach students about surface area and volume by challenging them to design a more environmentally friendly package for something they use, and send the design to the company. This places the seemingly abstract notion of equations into an actionable and meaningful context.
There is another angle for engaging students, which is less often discussed: beauty.
By the time material reaches the page of a textbook, it has been isolated from the puzzle that spurred it and from the context which makes it meaningful. As a result, students must memorize the names of various parts of a cell and learn to mechanically manipulate equations, without a grain of interest or joy. It’s no wonder that people do not look favorably on this dry material.
And yet, what often drives researchers in a given discipline is the inherent beauty and curiosity they feel about the subject matter. How can we put this beauty front and center? For a fast-paced example of math’s undeniable beauty take a look at any of the videos of Vi Hart (some of my favorites are the ones on plants, hexaflexagons, or the mobius strip).
In Alan Kay’s ted talk (mentioned above) he tells the story of a teacher who asked her 6 year old students to choose a shape, and make a larger version of that shape out of those shapes (for example a rhombus made of rhombuses). She then had them fill out a chart about how many pieces they needed to add to the shape before to make it the next shape, and how many pieces total the shape took up.
She then led the students to come together and share their results. They realized that even though they had chosen different shapes, the higher level patterns were the same; the students were baffled.
This result brought with it so many more mathematical questions to explore than answers to end up at. Without knowing the term “differential equations,” these 6 year olds experienced the beauty of math in a way that many college students (who do know this term) never get to experience.
To engage students and help them to learn material more deeply, we can up-end the way we normally teach all subjects, to highlight their beauty, their relevance, and to place their challenges front and center.
References & Further Reading
- Freeman, S., Eddy, S. L., McDonough, M., Smith, M. K., Okoroafor, N., Jordt, H., & Wenderoth, M. P. (2014). Active learning increases student performance in science, engineering, and mathematics. Proceedings of the National Academy of Sciences, 111(23), 8410-8415. [Paper]
- Bjork, R. A., & Linn, M. C. (2006). The science of learning and the learning of science. APS Observer, 19(3).
- Diemand-Yauman, C., Oppenheimer, D. M., & Vaughan, E. B. (2011). Fortune favors the (): Effects of disfluency on educational outcomes. Cognition, 118(1), 111-115. [Paper]
- D’Mello, S. (2012). Monitoring affective trajectories during complex learning. In Encyclopedia of the Sciences of Learning (pp. 2325-2328). Springer US.[Paper]
- Blake B., Pope, T. (2008) Developmental Psychology: Incorporating Piaget’s and Vygotsky’s Theories in Classrooms. Journal of Cross-Disciplinary Perspectives in Education 1(1) 59 – 67. [Paper]